|
|
 |
李克昭
Li, Ker-Chau
Institute
of Statistical Science Academia Sinica
Taipei 11529, Taiwan, R.O.C.
Tel: 886-2-27875696
E-mail: kcli@stat.sinica.edu.tw
|
Special links
Research Interests
- Bioinformatics, systems biology, lung cancer
studies,
High dimensional data analysis, Large
ensembles of time series, Medical image analysis,
Machine learning, Statistical graphics, Bayesian
computation, Regression, Censoring, Experimental design,
Survey sampling.
Li is best known for introducing sliced inverse
regression (SIR) and principal Hessian direction (PHD),
two fundamental dimension reduction methods for high
dimensional data analysis. Starting from 2000, his
research interest turned to the emerging field of
computation/mathematics/statistics in genome biology. In
2002, he published a paper in Proceedings of Academy of
Science, featuring the novel method of liquid
association (LA) for microarray gene expression
analysis. He is currently leading a research group in
UCLA and in Academia Sinica to continue the development
of methods for utilizing multiple sources of gene
expression profiling, genetic markers, complex disease
phenotypes and traits. A website
http://kiefer.stat2.sinica.edu.tw/LAP3 offers on-line
computation based on LA and related methods for gene
expression studies. He is also collaborating with Dr.
Pan Chyr Yang of National Taiwan University and his
colleagues on integrative cancer biology.
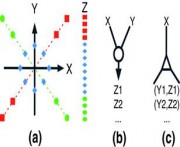
Liquid
association. (a) Association between genes X and Y as
mediated by gene Z. When gene Z is expressed at the high
level (red), a positive correlation between X and Y is
observed. The association changes as the expression of Z
is lowered. It eventually becomes a negative trend
(green). There are two basic ways (shown in panels b and
c) to apply the liquid association (LA) scoring system
to guide a genome-wide search. (b) When two genes X and
Y are given, compute LA score LA(X, Y|Z) for every gene
Z first and then output a short list of high score genes
Z1, Z2, and so on. (c) When only one gene X is given,
compute LA score LA(X, Y|Z) for every pair of genes X,Y
first and then output a short list of high score gene
pairs Y1,Z1, Y2,Z2, and so on. Li et al. Genome Biology
2007 8:R205 doi:10.1186/gb-2007-8-10-r205
- Liquid association. Correlation is a simple
and powerful method for analyzing gene expression
data.Two genes with positively correlated expression
profiles are likely to be functionally associated. They
may participate in the same biological process. However,
functionally associated genes may not be correlated for
a variety of reasons. For instance, they may not be
regulated at the transcription level. Another common
situation is that most genes have multiple functions.
Depending on the cellular needs, co-expressed genes may
become uncorrelated or even turn into contra-expressed.
Liquid association (LA), as opposed to "steady"
association, is designed to quantify the change of
correlation between two genes as a relevant cellular
state variable changes. There is no need to specify the
state variable explicitly. A highlighted example is the
elucidation of gene expression for the urea cycle in
yeast. This pathway controls both the biosynthesis and
degradation of the amino acid, arginine. LA is able to
find the correct genes which have to be turned on, as
well as the correct genes which have to be turned off at
the same time, so that any wasteful immediate
degradation of newly synthesized arginine can be
avoided.
- Sliced inverse regression (SIR). Many
statistical methods are known to suffer from urse of
dimensionality? they break down easily when dealing with
high dimensional data. How to reduce dimensionality is a
long-standing issue. Ad hoc methods such as principal
component analysis and partial least squares have been
advocated. Yet the associated issue about possible
nformation loss due to improper dimension reduction is
rarely addressed. The SIR methodology helps reshape this
area by presenting an effective dimension reduction
framework for theorizing both issues.
- Principal Hessian direction. Another effective
dimension reduction method.
Education
| 1981 |
Ph.D., Statistics, University of California,
Berkeley. (Advisor: Jack Kiefer) |
| 1975 |
B.S., Mathematics, National Taiwan
University |
Professional
Experience
| 2006-present |
Director and Distinguished Research
Fellow of Institute of Statistical Science, Academia
Sinica |
| 2000-2002 |
graduate vice chair, Statistics
Department, UCLA |
| 1999-present |
Professor, Statistics Department,
UCLA |
| 1989-present |
Professor, Mathematics Department,
UCLA |
| 1984-1989 |
Associate Professor, Mathematics
Department, UCLA |
| 1981-1984 |
Assistant Professor, Statistics
Department, Purdue University |
Professional
Activities
| 1999-2002 |
Co-Editor of Statistica Sinica |
| 1989-1994 |
Associate editor of Annals of Statistics |
| 1991-1999 |
Associate editor of Statistica Sinica |
| 1993-2001 |
Associate editor of Computational Statistics |
Honors
| 2003 |
Medallion Lecturer, IMS; 1993 Guggenheim
Fellow |
| 1991 |
NSF/ASA/NIST fellow; 1990 JASA theory and
methods Editor's invited speaker in Joint Statistical
Meetings |
| 1989 |
IMS Fellow; 1981 elected member of Phi Beta
Kappa |
| 1981 |
B. Friedman Memorial Prize in Applied
Mathematics, U.C. Berkeley |
Selected Publications
[1] Tomohiro Ando, Ker-Chau Li, 2017, “A weight-relaxed model averaging approach for high dimensional generalized linear models”, ANNALS OF STATISTICS, 45(6), 2654-2679. (SCIE) (IF: 2.65; SCI ranking: 13.7%)
[2] Chen HY, Yu SL, Ho BC, Su KY, Hsu YC, Chang CS, Li YC, Yang SY, Hsu PY, Ho H, Chang YH, Chen CY, Yang HI, Hsu CP, Yang TY, Chen KC, Hsu KH, Tseng JS, Hsia JY, Chuang CY, Yuan S, Lee MH, Liu CH, Wu GI, Hsiung CA, Chen YM, Wang CL, Huang MS, Yu CJ, Chen KY, Tsai YH, Su WC, Chen HW, Chen JJ, Chen CJ, Chang GC, Yang PC, Li KC*., 2015, “R331W Missense Mutation of Oncogene YAP1 Is a Germline Risk Allele for Lung Adenocarcinoma With Medical Actionability”, JOURNAL OF CLINICAL ONCOLOGY, 33(20), 2303-2310. (SCIE) (IF: 32.956; SCI ranking: 2%)
[3] Tomohiro Ando & Ker-Chau Li* , 2014, “A model-averaging approach for high-dimensional”, Journal of the American Statistical Association, 109(505), 254-265. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[4] Yi-Chiung Hsu, Hsuan-Yu Chen, Shinsheng Yuan, Sung-Liang Yu, Chia-Hung Lin, Guani Wu, Pan-Chyr Yang and Ker-Chau Li*, 2013, “Genome-wide analysis of three-way interplay between gene expression, cancer cell invasion and anti-cancer compound sensitivity”, BMC Medicine, 11, 106. (SCIE) (IF: 6.782; SCI ranking: 9.1%)
[5] Shinsheng Yuan, Sung-Liang Yu, Hsuan-Yu Chen, Yi-Chiung Hsu, Kang-Yi Su, Huei-Wen Chen, Chih-Yi Chen, Chong-Jen Yu, Jin-Yuan Shih, Yih-Leong Chang, Chiou-Ling Cheng, Chung-Ping Hsu, Jiun-Yi Hsia, Chien-Yu Lin, Guani Wu, Chia-Hsin Liu, Chin-Di Wang, Kang-Chung Yang, Yi-Wei Chen, Yi-Ling Lai, Chu-Chun Hsu, Tai-Ching Lin, Tsung-Ying Yang, Kun-Cheieh Chen, Kuo-Hsuan Hsu, Jeremy J.W. Chen, Gee-Chen Chang, Ker-Chau Li*, and Pan-Chyr Yang, 2011, “Clustered Genomic Alterations in Chromosome 7p Dictate Outcomes and Targeted Treatment Responses of Lung Adenocarcinoma With EGFR-Activating Mutations”, JOURNAL OF CLINICAL ONCOLOGY, 29(25), 3535-3442. (SCIE) (IF: 32.956; SCI ranking: 2%)
[6] Xuelian Wei and Ker-Chau Li* , 2010, “Exploring the within- and between-class correlation distributions for tumor classification”, Proceedings of the National Academy of Sciences of the United States of America, 107(15), 6737-6742. (SCIE) (IF: 9.412; SCI ranking: 11.3%)
[7] Yijing Shen, Wei Sun, and Ker-Chau Li*, 2010, “Dynamically weighted clustering with noise set”, Bioinformatics, 26(3), 341-347. (SCIE) (IF: 5.61; SCI ranking: 5.1%,7.8%,12.8%)
[8] Yi-Chiung Hsu, Shinsheng Yuan, Hsuan-Yu Chen, Sung-Liang Yu, Chia-Hsin Liu,Pin-Yen Hsu, Guani Wu,Chia-Hung Lin, Gee-Chen Chang, Ker-Chau Li*, and Pan-Chyr Yang, 2009, “A four-gene signature from NCI-60 cell line for survival prediction in non–small cell lung cancer”, Clinical Cancer Research, 15(23), 7309-7315. (SCIE) (IF: 10.107; SCI ranking: 7.4%)
[9] Ching-Ti Liu; Shinsheng Yuan; Ker-Chau Li*, 2008, “Patterns of co-expression for protein complexes by size in Saccharomyces cerevisiae”, Nucleic Acids Research, 37(2), 526-532. (SCIE) (IF: 11.502; SCI ranking: 5.1%)
[10] Sung-Liang Yu, Hsuan-Yu Chen, Gee-Chen Chang, Chih-Yi Chen, Huei-Wen Chen, Sher Singh, Chiou-Ling Cheng, Chong-Jen Yu, Yung-Chie Lee, Han-Shiang Chen, Te-Jen Su, Ching-Cheng Chiang, Han-Ni Li, Qi-Sheng Hong, Hsin-Yuan Su, Chun-Chieh Chen, Wan-Jiun Chen, Chun-Chi Liu, Wing-Kai Chan,Wei J. Chen, Ker-Chau Li, Jeremy J.W. Chen, and Pan-Chyr Yang, Li, Chen, Yang contributed equally to directing the research, 2008, “MicroRNA Signature Predicts Survival and Relapse in Lung Cancer”, Cancer Cell, 13, 48-57. (SCIE) (IF: 26.602; SCI ranking: 2.9%,2.1%)
[11] Li, K.C.*, Palotie A*, Yuan, S, Bronnikov, D., Chen D., Wei X., Choi, O., Saarela J., Peltonen L. , 2007, “Finding disease candidate genes by liquid association”, Genome Biology, 8(10), R205-R205. (SCIE) (IF: 10.806; SCI ranking: 3.2%,4.5%)
[12] Yuan, S., and Li. K.C.*, 2007, “Context-dependent Clustering for Dynamic Cellular State Modeling of Microarray Gene Expression”, Bioinformatics, 23(22), 3039-3047. (SCIE) (IF: 5.61; SCI ranking: 5.1%,7.8%,12.8%)
[13] Li, K.C.*, Ching-Ti Liu, Wei Sun, Shinsheng Yuan and Tianwei Yu, 2004, “A system for enhancing genome-wide co-expression dynamics study”, Proceedings of the National Academy of Sciences of the United States of America, 101, 15561-15566. (SCIE) (IF: 9.412; SCI ranking: 11.3%)
[14] Xie, J., Li, K.C., and Bina, M., 2004, “A Bayesian Insertion/Deletion Algorithm for Distant Protein Motif Searching via Entropy Filtering”, Journal of the American Statistical Association, 99, 409-420.
[15] Li, K.C., Aragon, Y, Shedden, K. and Thomos-Agan C., C., 2003, “Dimension reduction for multivariate response data”, Journal of the American Statistical Associations, 98, 99-106. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[16] Li, K.C., 2002, “Genome-wide co-expression dynamics: theory and application”, Proceedings of the National Academy of Sciences of the United States of America, 99, 16875-16880. (SCIE) (IF: 9.412; SCI ranking: 11.3%)
[17] Li, K.C. and Shedden. K., 2002, “Identification of shared common components in large ensembles of time series using dimension reduction”, Journal of the American Statistical Association, 97, 759-765. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[18] Li, K.C., Lue, H.H, and Chen, C.H., 2000, “Interactive tree-structured regression via principal Hessian directions”, Journal of the American Statistical Association, 95, 547-560. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[19] Li, K. C. , 1997, “Nonlinear confounding in high dimensional regression”, Annals of Statistics, 25, 577-612. (SCIE) (IF: 2.65; SCI ranking: 13.7%)
[20] Lee, J. J., Li, K. C. and Elashoff, R. M., 1993, “On re-censoring for censored paired data”, Journal of the American Statistical Association, 88, 104-118. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[21] Hall, P. and Li, K. C.*, 1993, “On almost linearity of low dimensional projection from high dimensional data”, Annals of Statistics, 21, 867-889. (SCIE) (IF: 2.65; SCI ranking: 13.7%)
[22] Carroll, R. J. and Li, K. C.*, 1992, “Measurement error regression with unknown link: dimension reduction and data visualization”, Journal of the American Statistical Association, 87, 1040-1050. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[23] Li, K. C. , 1992, “On principal Hessian directions for data visualization and dimension reduction: another application of Stein's lemma”, Journal of the American Statistical Association, 87, 1025-1039. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[24] Li, K. C. , 1991, “Sliced inverse regression for dimension reduction, with discussions”, Journal of the American Statistical Association, 86, 316-342. (SCIE) (IF: 3.989; SCI ranking: 3.2%)
[25] Li, K. C, 1989, “Honest confidence regions for nonparametric regression”, Annals of Statistics, 17, 1001-1008. (SCIE) (IF: 2.65; SCI ranking: 13.7%)
[26] Li, K. C. , 1985, “From Stein's unbiased risk estimates to the method of generalized cross validation”, Annals of Statistics, 13, 1352-1377. (SCIE) (IF: 2.65; SCI ranking: 13.7%)
Full list of publications
|
|